Золотое сечение
Эта идеальная пропорция, к которой каким-то образом стремятся природные объекты, создаются и описываются явления в искусстве, музыке. По сути, золотое сечение как связующее звено математических отношений, в приближениях иррационального числа рациональными числами, в бесконечных цепных дробях, в геометрии правильной пятиконечной звезды. Приближенное округление в процентах значения золотого деления дает результат отношения 62 % и 38%.
Проявление золотого сечения чисел Фибоначчи выражается в результате деления двух соседних элементов последовательности, который сходится (при возрастании m) и приближается к 1,618. Разделить на 2 целые доли с лучшим приближением к золотому сечению помогут элементы последовательности Фибоначчи. Например: в числе 13 разделяется на 8 и 5, в числе 21 — 13, 8.
Поделим отрезок LP(b) так, что точка N выполнит золотое сечение его таким образом, что LN: LP = NP:LN. Пусть LN=y (большая часть), тогда NP= b-y. Получается y:b=(b-y):y, т.е. y2=b*(b-y). Для определения y следует провести на отрезке дополнительное построение прямоугольного треугольника, используя среднее геометрическое длин отрезка и теорему Пифагора. Вычисляется значение y=( -1):2*b=0.62*b приближенно (t=0,618034).
Это лишь одно такое удивительное число, что обратное ему больше его самого ровно на 1, 1:t=1+t=1,618034. Решение уравнения t2 + t – 1 = 0 имеет единственный плюсовой корень. Используя это свойство числа, преобразовав выражение можно перейти к формуле числа t как бесконечной цепной дроби.
Золотая пропорция является иррациональной величиной. Числа Фибоначчи отражают целочисленные величины, отношение которых приближается к золотому делению. Эти две закономерности отражают неразрывность единых начал — непрерывного и дискретного.
Спираль Фибоначчи и спираль «золотого сечения»
На основе чисел Фибоначчи и «золотого сечения» можно построить спирали. Иногда эти две фигуры отождествляют, но точнее говорить о двух разных спиралях.
Спираль Фибоначчи строят так:
чертят два квадрата (одна сторона общая), длина сторон равна 1 (сантиметр, дюйм или клетка — неважно). Получается поделенный надвое прямоугольник, длинная сторона которого равна 2;
к длинной стороне прямоугольника пририсовывают квадрат со стороной 2. Получается изображение прямоугольника, поделенного на несколько частей
Длинная сторона его равна 3;
процесс продолжают сколь угодно долго. При этом новые квадраты «присоединяют» подряд только по или только против часовой стрелки;
в самом первом квадратике (со стороной 1) чертят от угла до угла четвертинку окружности. Затем без перерыва чертят подобную линию в каждом следующем квадрате.
Получается изображение прямоугольника, поделенного на несколько частей. Длинная сторона его равна 3;
процесс продолжают сколь угодно долго. При этом новые квадраты «присоединяют» подряд только по или только против часовой стрелки;
в самом первом квадратике (со стороной 1) чертят от угла до угла четвертинку окружности. Затем без перерыва чертят подобную линию в каждом следующем квадрате.
В итоге получают красивую спираль, радиус которой постоянно и пропорционально увеличивается.
Спираль «золотого сечения» рисуют наоборот:
- строят «золотой прямоугольник», стороны которого соотносятся в одноименной пропорции;
- выделяют внутри прямоугольника квадрат, стороны которого равны короткой стороне «золотого прямоугольника»;
- при этом внутри большого прямоугольника окажется квадрат и прямоугольник поменьше. Тот, в свою очередь, тоже окажется «золотым»;
- малый прямоугольник делят по тому же принципу;
- процесс продолжают сколь угодно долго, располагая каждый новый квадрат спиралеообразно;
- внутри квадратиков рисуют соединенные между собой четверти окружности.
Так получается логарифмическая спираль, которая растет в соответствии с золотым сечением.
Спираль Фибоначчи и «золотая» очень похожи. Но есть главное отличие: у фигуры, построенной по последовательности пизанского математика, есть начальная точка, хотя конечной — нет. А вот «золотая» спираль закручивается «внутрь» до бесконечно малых чисел, как и раскручивается «во вне» до бесконечно больших.
Золотое сечение
Золотое сечение является делением целого на части, соотносящиеся по принципу: большее относится к меньшему аналогично тому, как общая величина относится к большей части.
Впервые о золотом сечении упоминает Евклид (трактат «Начала» прим. 300 лет до н.э.), говоря и построении правильного прямоугольника. Однако более привычное понятие было введено немецким математиком Мартином Омом.
Приблизительно золотое сечение можно представить в качестве пропорционального деления на две разные части, к примеру, на 38% и 68%. Численное же выражение золотого сечения равно примерно 1,6180339887.
На практике золотое сечение используется в архитектуре, изобразительном искусстве (посмотрите работы Леонардо да Винчи), кино и других направлениях. На протяжении долгого времени, впрочем, как и сейчас, золотое сечение считалось эстетической пропорцией, хотя большинством людей оно воспринимается непропорциональным – вытянутым.
Вы можете попробовать оценить золотое сечение сами, руководствуясь следующими пропорциями:
- Длина отрезка a = 0,618
- Длина отрезка b= 0,382
- Длина отрезка c = 1
- Соотношение c и a = 1,618
- Соотношение c и b = 2,618
Теперь же применим золотое сечение к числам Фибоначчи: берём два соседних члена его последовательности и делим большее на меньшее. Получаем примерно 1,618. Если же возьмём то же самое большее число и поделим его на следующее большее за ним, то получим примерно 0,618. Попробуйте сами: «поиграйте» с числами 21 и 34 или какими-то другими. Если же провести этот опыт с первыми числами последовательности Фибоначчи, то такого результата уже не будет, т.к. золотое сечение «не работает» в начале последовательности. Кстати, чтобы определить все числа Фибоначчи, нужно знать всего лишь три первых последовательных числа.
И в заключение ещё немного пищи для ума.
Задача Фибоначчи с кроликами
Для выполнения задачи автором были поставлены следующие условия: есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью – со второго месяца жизни они производят новую пару кроликов – тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.
Задача: определить количество кроликов через год.
Решение:
У нас есть:
- Одна пара кроликов в начале первого месяца, которая спаривается в конце месяца
- Две пары кроликов во втором месяце (первая пара и потомство)
- Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)
- Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)
Количество кроликов в месяц «n» = количеству кроликов прошлого месяца + количество новых пар кроликов, другими словами, вышеназванная формула: Fn = Fn-1 + Fn-2. Отсюда получается рекуррентная числовая последовательность (о рекурсии мы скажем далее), где каждое новое число соответствует сумме двух предыдущих чисел:
1 месяц: 1 + 1 = 2
2 месяц: 2 + 1 = 3
3 месяц: 3 + 2 = 5
4 месяц: 5 + 3 = 8
5 месяц: 8 + 5 = 13
6 месяц: 13 + 8 = 21
7 месяц: 21 + 13 = 34
8 месяц: 34 + 21 = 55
9 месяц: 55 + 34 = 89
10 месяц: 89 + 55 = 144
11 месяц: 144 + 89 = 233
12 месяц: 233+ 144 = 377
И эта последовательность может продолжаться бесконечно долго, но учитывая, что задачей является узнать количество кроликов по истечении года, получается 377 пар.
Здесь важно также заметить, что одним из свойств чисел Фибоначчи является то, что если сопоставить две последовательные пары, а затем разделить большую на меньшую, то результат будет двигаться по направлению к золотому сечению, о котором мы также скажем ниже. Пока же предлагаем вам ещё две задачи по числам Фибоначчи:
Пока же предлагаем вам ещё две задачи по числам Фибоначчи:
- Определить квадратное число, о котором известно только, что если отнять от него 5 или прибавить к нему 5, то снова выйдет квадратное число.
- Определить число, делящееся на 7, но при условии, что поделив его на 2, 3, 4, 5 или 6 в остатке будет 1.
Такие задачи не только станут отличным способом развития ума, но и занимательным времяпрепровождением. О том, как решаются эти задачи, вы также можете узнать, поискав информацию в Интернете
Мы же не будем заострять на них внимание, а продолжим наш рассказ
Что же такое рекурсия и золотое сечение?
В подсолнухе и в ухе
С рядом Фибоначчи и числом Фи в геометрии связана логарифмическая спираль, которая разворачивается по принципу золотого сечения. Её можно вписать в систему вложенных друг в друга «золотых» прямоугольников с отношением сторон, равным Фи, или описать вокруг неё. А удивляет то, что такие модели часто встречаются в природе. По образу спирали Фибоначчи построены раковины моллюсков Nautilus pompilius и окаменелых аммонитов. Их рост хорошо описывается на основе числа Фи с коэффициентом 2.
Отношение длин трёх витков спирали уха человека точно соответствует Фи и такие же параметры — у раковин некоторых улиток. Недавно узнали, что золотая и другие логарифмические спирали встречаются в роговичном эпителии мышей.
Статья по теме
ДНК-машина вместо хлебницы. Какие суперизобретения скоро станут массовыми
Ещё Леонардо да Винчи и знаменитый немецкий учёный Кеплер обращали внимание на винтовое расположение листьев у растений, напоминающее спираль. Так же растут лепестки у цветов, семечки в подсолнечнике, шишки у хвои, чешуйки на плодах ананаса
Эту закономерность в ботанике называют филлотаксисом, и в формулах листорасположения тоже встречаются числа Фибоначчи, расположенные через одно. Такие свойства определяет генетика, уходящая корнями на клеточный и молекулярный уровни. А полипептидные цепи в молекуле ДНК тоже имеют винтовое расположение. Есть данные, что соотношение длины и ширины у них несёт в себе формулу золотого сечения.
Тот же принцип виден и в строении галактик. Например, наш Млечный Путь имеет несколько рукавов, растущих по принципу логарифмической спирали с шагом примерно 12 градусов. Великий поэт Гёте, который также был естествоиспытателем, считал спиральность одним из характерных признаков всех организмов, проявлением самой сокровенной сущности жизни. И, может быть, не случайно символ спирали присутствовал в культуре многих коренных народов Земли.
Драконы, чупакабры и инопланетяне. Говорим о загадках и тайнах Беларуси
Подробнее
Заблуждения, связанные с числами Фибоначчи
Благодаря современной поп-культуре с этой числовой последовательностью связано множество популярных мифов:
- Универсальность. Во многих источниках числа Фибоначчи и золотая спираль позиционируются как универсальный закон мироздания, с помощью которого можно описать любой природный процесс или объекты, от расположения лепестков цветка до формы спиральных галактик. Хотя в отношении многих природных явлений это действительно так, принцип не является всеобъемлющим: например, те же рукава спиральных галактик или раковина моллюска наутилуса закручены по логарифмической спирали, которая, хоть и близка по форме к золотой, все же ей не является.
- Идеальность. Распространено мнение, что золотое сечение и спираль Фибоначчи описывают идеальные пропорции. Однако исследования показали, что объекты, построенные по этому принципу (например человеческое тело), при демонстрации обычным людям воспринимаются обычно как диспропорциональные, вытянутые. Отсюда является заблуждением и утверждение, что все великие художники эпохи Возрождения и последующих времен использовали принцип золотой спирали в своих работах. Такие эксперименты действительно случались, но это не было распространенным явлением.
- Практическая применимость. Еще один миф говорит о том, что использование золотого сечения и чисел Фибоначчи в любом сфере деятельности дает положительный результат. Но, например, криптографы знают, что метод Фибоначчи с запозданием не является идеальным способом усилить шифрование — многие генераторы случайных чисел на его основе либо медленно работают, либо имеют недостаточный порог устойчивости к взлому. А использование принципов золотого сечения в архитектуре или промышленном дизайне редко сочетается с оптимизацией производства.
Вместе с тем нельзя отрицать большую роль фибоначчиевых чисел в развитии фундаментальной и прикладной математики, информатики и смежных с ними наук. Разработанные на основе золотой спирали методы и технологии широко применяются в разных областях человеческой жизни, от сугубо научных до прикладных, таких как компьютерная графика, криптография, программирование, обработка данных и т.д.
Числа Фибоначчи в природе
Подсолнухи являются отличными примерами последовательности Фибоначчи, потому что семена в центре цветка организованы в два набора спиралей — короткие, идущие по часовой стрелке от центра, и более длинные — против часовой стрелки. Если считать спирали последовательно, то, видимо, всегда найдутся числа Фибоначчи.
Последовательность Фибоначчи можно также увидеть в форме или разделении ветвей дерева. Основной ствол будет расти до тех пор, пока он не создаст ветвь, которая создает две точки роста. Затем один из новых стеблей разветвляется на два, в то время как другой находится в состоянии покоя. Такая картина ветвления повторяется для каждого из новых стеблей. Корневая система и даже водоросли также демонстрируют эту закономерность.
Ветви дерева демонстрируют последовательность Фибоначчи.
Вот еще несколько примеров, где вы можете найти спираль Фибоначчи в природе.
Неудивительно, что спиральные галактики также следуют знакомой схеме Фибоначчи. Млечный Путь имеет несколько спиральных рукавов, каждый из которых представляет логарифмическую спираль около 12 градусов.
Формула для n-го числа Фибоначчи
Формула через радикалы
Существует замечательная формула, называемая по имени французского математика Бине (Binet), хотя она была известна до него Муавру (Moivre):
Эту формулу легко доказать по индукции, однако вывести её можно с помощью понятия образующих функций или с помощью решения функционального уравнения.
Сразу можно заметить, что второе слагаемое всегда по модулю меньше 1, и более того, очень быстро убывает (экспоненциально). Отсюда следует, что значение первого слагаемого даёт «почти» значение . Это можно записать в строгом виде:
где квадратные скобки обозначают округление до ближайшего целого.
Впрочем, для практического применения в вычислениях эти формулы мало подходят, потому что требуют очень высокой точности работы с дробными числами.
Матричная формула для чисел Фибоначчи
Нетрудно доказать матричное следующее равенство:
Но тогда, обозначая
получаем:
Таким образом, для нахождения -го числа Фибоначчи надо возвести матрицу в степень .
Вспоминая, что возведение матрицы в -ую степень можно осуществить за (см. Бинарное возведение в степень), получается, что -ое число Фибоначчи можно легко вычислить за c использованием только целочисленной арифметики.
Числа Фибоначчи — это что?
Поразителен тот факт, что при делении каждого последующего числа числовой последовательности на предыдущее получается число, стремящееся к 1,618.
Обнаружил эту загадочную последовательность счастливчик математик средневековья Леонардо Пизанский (более известный под именем Фибоначчи). До него Леонардо да Винчи обнаружил в строении тела человека, растений и животных удивительным образом повторяющуюся пропорцию Фи = 1,618. Это число (1,61) ученые еще называют «Числом Бога».
До Леонардо да Винчи эта последовательность чисел была известна в Древней Индии и Древнем Египте. Египетские пирамиды построены с применением пропорции Фи = 1,618.
Но и это еще не все, оказывается законы природы Земли и Космоса каким-то необъяснимым образом подчиняются строгим математическим законам последовательности чисел Фидоначчи.
Например, и ракушка на Земле, и галактика в Космосе построены с применением чисел Фибоначчи. Абсолютное большинство цветов имеет 5, 8, 13 лепестков. В подсолнухе, на стеблях растений, в закрученных вихрях облаков, в водоворотах и даже в графиках изменения курсов валют на Форексе, всюду работают числа Фибоначчи.
-
Посмотрите простое и занимательное пояснение, что такое последовательность чисел Фибоначчи и Золотое сечение в этом КОРОТКОМ ВИДЕО (6 минут):
https://youtube.com/watch?v=kayX8XTjL9E
Что такое Золотое сечение или Божественная пропорция?
Итак, что такое Золотое сечение или Золотая или Божественная пропорция? Фибоначчи также обнаружил, что последовательность, которая состоит из квадратов чисел Фибоначчи является еще большей загадкой. Попробуем графически изобразить в виде площади последовательность:
1², 2², 3², 5², 8²…
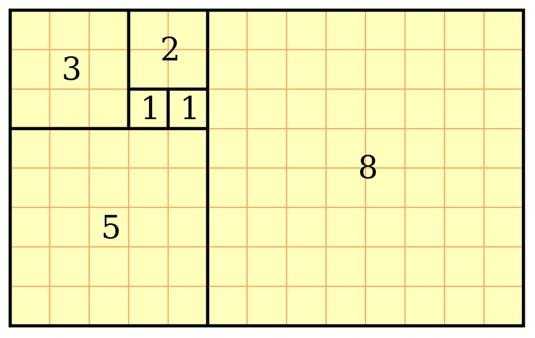Если вписать спираль в графическое изображение последовательности квадратов чисел Фибоначчи, то мы получим Золотое сечение, по правилам которого построено все во вселенной, включая растения, животных, спираль ДНК, человеческое тело, … Список этот можно продолжать до бесконечности.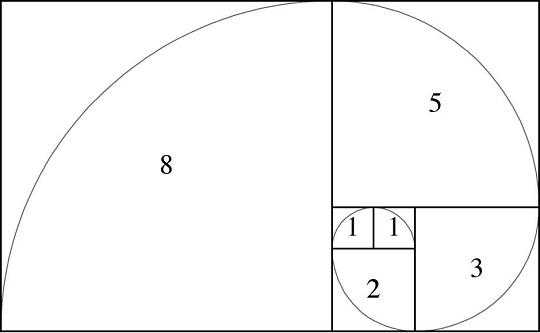
Золотое сечение и Числа Фибоначчи в природе ВИДЕО
Предлагаю посмотреть короткий фильм (7 минут), в котором раскрываются некоторые загадки Золотого сечения.
При размышлениях о законе чисел Фибоначчи, как о первостепенном законе, который управляет живой и неживой природой, появляется вопрос: Эта идеальная формула для макромира и микромира возникла сама или ее кто-то создал и удачно применил?
Что ВЫ думаете по этому поводу? Давайте вместе подумаем над этой загадкой и быть может мы приблизимся к тайне мироздания.
Очень надеюсь, что статья была полезной для Вас и Вы узнали, что это такое Золотое сечение *и Числа Фибоначчи? До новых встреч на страницах блога, подписывайтесь на блог. Форма подписки — под статьей.
Не могу не поделиться с Вами коротким документальным фильмом — ученые обнаружили загадочную связь между кодом ДНК и числом Бога.
-
Спираль Фибоначчи – загадка природы (фото)
Математические науки не знают второй формы, способной сравниться своими свойствами со спиралью, получившей свои оригинальные свойства благодаря положенному в базис структуры Золотое сечение. Напомним, что формула имеет следующий вид: ( a + b )/ a = a / b.
Известный золотой прямоугольник приобрёл своё название именно в честь того, что он обладает как раз таким соотношением сторон — отношение его длинных сторон к меньшим равно 1,168:1.
Рисунок 4. Спираль Фибоначчи проявляется в природе – это загадка последовательности чисел знаменитого ряда Фибоначчи.
Одним из необыкновенных свойств золотого прямоугольника является то, что если от такой фигуры отделить квадрат, с большей стороной равной длине малой стороны прямоугольника, в результате будет получен ещё один золотой прямоугольник, но меньший по площади.
Причём эту операцию можно повторять постоянно, и каждый раз её итогом будет получение золотого прямоугольника ещё меньшего размера. Интересно, что расположение этих прямоугольников будет соответствовать логарифмической спирали, играющей ключевую роль в математических моделях объектов, которые вполне реально обнаружить в природе.
Обычно спиральную структуру наблюдают в закономерности позиций семян подсолнечника, структуре лепестков некоторых видов цветов, в необычной геометрии ракушек.
У подавляющего большинства улиток раковина обладает именно спиралевидной формой. Поскольку эти существа не обладают разумом, они не могут владеть элементарными математическими знаниями, достаточными для создания собственной раковины подобной формы. Многие учёные не могут точно определить причину, по которой эти моллюски сумели выбрать такую необычную форму существования.
Ясно здесь только, что подобное развитие не может считаться случайным стечением обстоятельств, и сама по себе подобная гипотеза будет выглядеть глупо. Это явно осознанное творение.
Спирали легко обнаружить и в теле человека — к такому примеру можно отнести человеческое ухо, внутренне ухо которого так же включает в себя орган, известный как «Улитка», предназначенный для превращения звуковой вибрации в нейронные сигналы. Схожая с костью, эта структура внутри заполнена жидкостью и внешне напоминает улитку, традиционно соответствующую золотым пропорциям.
Спирали также можно найти на ладонях и пальцах человека, элементарно сняв отпечатки.
В животном мире встретить огромное количество спиралевидных форм можно буквально повсюду — закрученные рога и бивни некоторых видов животных, когти и клювы некоторых видов птиц.
Форму спирали принимает и ураган, и лучше всего это можно наблюдать на снимках, сделанных орбитальной космической станцией, глядя, как скручиваются облака циклона.
В волнах, закручивающихся на морской или океанской глади, ясно виден математический график золотого сечения Фибоначчи в природе со значениями 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55. Не стоит так же забывать о водоворотах, или, по крайней мере, о воде, сливающейся в раковине в водосточную трубу.
Рисунок 5. Загадки спирали Фибоначчи в природе до сих пор не разгаданы.
К слову, золотое сечение угадывается даже в форме галактики.
Спираль заслуженно носит звание «Кривой жизни», ведь её причудливая форма имеет место и угадывается во многих областях. Это настоящий символ эволюции, ибо нет такого объекта, чьё развитие не двигалось бы по спирали.
И лишнее тому подтверждение — существование Золотого прямоугольника, что при разбиении на более мелкие прямоугольники в соответствии с последовательностью Фибоначчи с последующим разделением их в идентичной пропорции и далее, будет получена система под говорящим названием спираль Фибоначчи.
Краткая биография
- В 1200 г. математик вернулся в Пизу и решил заняться обобщением полученной им информации и написать такую книгу, которая содержала бы максимальное количество данных для обучения арифметике.
- В 1202 г. он начал писать там главный труд своей жизни – «Книгу абака». Книга была посвящена десятичной арифметике. Эта книга ценна еще и тем, что она является практически единственным источником, содержащим автобиографические данные. Именно в этой книге математик рассказал о том, что привело его к счетному искусству. Он поведал и ценности научных споров, которым был обучен также благодаря путешествиям с отцом по странам Востока. Он искренне восхищался методом индийцев и пытался донести его до европейцев, чтобы они не были ограничены в информации об искусстве вычислений. К сожалению, эту информацию нельзя назвать абсолютно достоверной, поскольку текст, написанный на латыни, переписывался. Этот труд математик начал писать не только с целью помощи математикам, но и для просвещения купцов и всех тех, кто имел дело с деньгами и, соответственно, с вычислениями.
- В 1220 г. появилась книга «Практика геометрии». Она содержит 7 частей. В ней расписаны теоремы с измерительными методами и доказательства к ним, в том числе, собственные доказательства Фибоначчи. Так, Леонардо сделал первое дошедшее до наших дней доказательство пересечения трех медиан треугольника в одной точке.
- Около 1225 г. Доминикус Хиспанус предложил Фридриху II пригласить Леонардо во время посещения Пизы. Так и было сделано, и один из придворных философов Фридриха II Иоанн Палермский предлагал Леонардо задачи для решения. Эти своеобразные математические турниры способствовали тому, чтобы сам император заинтересовался гением математика.
- В 1225 г. Пизанский получил надежное покровительство правителя Священной Римской империи и начал жить при императорском дворе.
- В 1225 г. вышел трактат «Цветок», в котором Леонардо исследовал кубическое уравнение, которое, вероятнее всего, было заимствовано Иоанном Палермским из трактата Омара Хайяма.
- В том же году вышла «Книга квадратов» с неопределенными квадратными уравнениями и их решениями. Одна из задач книги, как и уравнение из трактата «Цветок», была предложена Иоанном Палермским.
- В том же году Леонардо написал письмо Теодорусу (философ Теодорус Физикус, придворный ученый Фридриха II).
- В 1228 г. «Книга абака» вышла повторно с дополнениями. Именно рукопись этого года сохранилась до нашего времени. В книге 15 глав и в ней собраны все сведения об алгебре и арифметике, имеющиеся в то время. Эта книга заинтересовала императора Священной Римской империи Фридриха II и ряд ученых, находившихся при дворе.
- Среди работ великого математика есть еще две, даты которых неизвестны, а сами работы утеряны. Это «Di minor guise» и «Комментарии к книге X «Начал» Евклида.
- После 1228 г. сведения о Фибоначчи резко обрываются, как будто в этот период времени ничего не происходило.
- Существует предположение, согласно которому, прозвище «Фибоначчи» появилось в 1838 г., и дал его Гийом Либри.
- В 1240 г. Леонардо стал получать пенсию за заслуги перед городом Пиза (Пизанская республика).
- Великий математик ушел из жизни около 1250 г. Портретов Леонардо, написанных при его жизни, не сохранилось. Кроме того, он оставил слишком мало автобиографических данных.
Фрагмент книги абака
Слайды и текст этой презентации
ЛЕОНАРДО ПО ПРОЗВИЩУ ФИБОНАЧЧИ
Выполнили ученицы 5 «А» классаСредней школы № 153Фрыгина Ксения и Родина Евгения
Леона́рдо Пиза́нский — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи. Является создателем чисел Фибоначчи.
Отец Фибоначчи по торговым делам часто бывал в Алжире, и Леонардо изучал там математику у арабских учителей. Позже Фибоначчи посетил Египет, Сирию, Византию, Сицилию. Он ознакомился с достижениями античных и индийских математиков в арабском переводе. На основе усвоенных им знаний Фибоначчи написал ряд математических трактатов, представляющих собой выдающееся явление средневековой западноевропейской науки. Труд Леонардо Фибоначчи «Книга абака» способствовал распространению в Европе позиционной системы счисления, более удобной для вычислений, чем римская нотация; в этой книге были подробно исследованы возможности применения индийских цифр, ранее остававшиеся неясными, и даны примеры решения практических задач, в частности, связанных с торговым делом. Позиционная система приобрела в Европе популярность в эпоху Возрождения.
В век Фибоначчи возрoждение было еще далеко, однако история даровала Италии краткий промежуток времени. Руководил этим Фридрих II, император(с 1220 года) Священной Римской империи. Воспитанный в традициях южной Италии Фридрих II был внутренне глубоко далек от своих предков. Столь любимые его дедом рыцарские турниры Фридрих II совсем не признавал. Вместо этого он любил менее кровавые, математические соревнования, на которых противники обменивались не ударами, а задачами.
Золотое сечение
Длина отрезка a = 0,618Длина отрезка b= 0,382Длина отрезка c = 1Соотношение c и a = 1,618Соотношение c и b = 2,618
«Liber abaci», или трактат по арифметике (а именно так можно истолковать название, поскольку под «абаком» Леонардо понимал не счетную доску, а арифметику), отличалась полнотой охвата и глубиной изложения. В ней подробно разъяснялись не только азы науки о числах и действиях над ними, но и основы учения об уравнениях, т.е. алгебры. Кроме того, в «Liber abaci» имелось большое количество задач практического содержания, иллюстрировавших различные приемы решения, как арифметические – тройное правило, правило товарищества, метод ложного положения и др., так и алгебраические, приводящие к одному или нескольким уравнениям.
Само изложение было словесным, лишенным символов и формул, а решение примеров и задач, носивших частный характер, сводилось к описанию действий, которые следовало применить в той или иной конкретной ситуации, и нередко сопровождалось разъяснениями или полезными комментариями автора.
Наибольший интерес представляет для нас сочинение «Kнига абака» («Liber Abaci»). Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течении нескольких следующих столетий. В частности, именно по этой книге европейцы познакомились с индусскими (арабскими) цифрами.В «Liber Abaci» Фибоначчи приводит свою последовательность чисел как решение математической задачи — нахождение формулы размножения кроликов. Числовая последовательность такова: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 (далее до бесконечности).
О жизненном пути самого Фибоначчи известно крайне мало. Но достоверно известно то, что его задачи пользовались огромнейшей популярностью в математических кругах в последующие века.
